1948. Топологическая сортировка

Задан ориентированный невзвешенный граф. Выполните топологическую сортировку его вершин.

Вход. В первой строке содержится количество вершин n (1 ≤ n ≤ 10⁵) и количество рёбер m (1 ≤ m ≤ 10⁵) в графе. В следующих m строках перечислены рёбра графа, каждое из которых задаётся парой чисел – номерами начальной и конечной вершины.

Выход. Если топологическая сортировка графа возможна, выведите любую из них в виде последовательности номеров вершин. Если граф невозможно топологически отсортировать, выведите -1.

Пример входа	Пример выхода
6 6 1 2 3 2 4 2 2 5 6 5 4 6	4 6 3 1 2 5

РЕШЕНИЕ

графы – топологическая сортировка

Анализ алгоритма

Задача топологической сортировки может быть решена с использованием поиска в глубину.

· Изначально все вершины помечены белым цветом.

· Когда обход в глубину достигает вершины, она становится серой.

· После завершения обработки вершина помечается чёрным цветом.

Порядок вершин в топологической сортировке соответствует обратному порядку их перехода в чёрный цвет. Другими словами, первая полностью обработанная вершина (при поиске в глубину) окажется последней в топологической сортировке, а последняя обработанная вершина – первой.

Вершины графа невозможно топологически отсортировать, если в графе присутствует цикл. В ориентированном графе это означает, что при обходе в глубину не должно быть рёбер, ведущих к серым вершинам, поскольку такое ребро указывает на цикл.

Пример

Граф, приведенный в примере, имеет следующий вид:

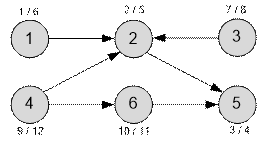
Возле каждой вершины v разместим метки d[v] / f[v], где d[v] – время начала обработки вершины, а f[v] – время завершения её обработки. Топологически отсортированные вершины располагаются в порядке убывания значений f[v].

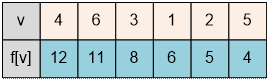
Реализация алгоритма

Поскольку количество вершин в графе велико, будем хранить граф в виде списка смежности g. Для хранения состояния вершин используем массив used:

· used[i] = 0, если вершина i еще не посещена (вершина белая);

· used[i] = 1, если вершина i посещена, но ее обработка еще не завершена (вершина серая);

· used[i] = 2, если вершина i уже обработана (вершина черная);

В процессе выполнения поиска в глубину будем добавлять вершины в массив top в порядке завершения их обработки. После завершения алгоритма массив top будет содержать вершины в порядке, обратном топологической сортировке.

vector<vector<int> > g;

vector<int> used, top;

Функция dfs выполняет обход графа в глубину, начиная с вершины v.

void dfs(int v)

{

Заходим в вершину v и помечаем её серым цветом.

used[v] = 1;

Перебираем все вершины to, в которые можно попасть из вершины v.

for (int to : g[v])

{

Если ориентированное ребро (v, to) ведет в серую вершину, это означает наличие цикла в графе. В этом случае устанавливаем flag = 1.

if (used[to] == 1) flag = 1;

Если вершина to еще не посещена, рекурсивно запускаем из неё поиск в глубину.

if (used[to] == 0) dfs(to);

}

Завершаем обработку вершины v. Помечаем её чёрным цветом и добавляем в массив top.

used[v] = 2;

top.push_back(v);

}

Основная часть программы. Читаем входные данные. Строим список смежности графа.

scanf("%d %d",&n,&m);

g.resize(n+1); used.resize(n+1);

for(i = 0; i < m; i++)

{

scanf("%d %d",&a,&b);

g[a].push_back(b);

}

Выполняем обход ориентированного графа в глубину.

flag = 0;

for(i = 1; i <= n; i++)

if (used[i] == 0) dfs(i);

Если при обходе в глубину обнаруживается цикл (установлен flag = 1), выводим -1.

if (flag == 1) printf("-1");

else

В противном случае выводим вершины графа в порядке, обратном их добавлению в массив top.

for(i = top.size() - 1; i >= 0; i--)

printf("%d ",top[i]);

printf("\n");

Реализация алгоритма – Кан

Входной граф храним в списке смежности g.

Входящие степени вершин храним в массиве InDegree.

Результат топологической сортировки заносим в массив top.

vector<vector<int> > g;

vector<int> InDegree, top;

deque<int> q;

Читаем количество вершин n и количество ребер m.

scanf("%d %d",&n,&m);

g.resize(n+1);

InDegree.resize(n+1);

Читаем m ребер графа.

for(i = 0; i < m; i++)

{

scanf("%d %d",&a,&b);

g[a].push_back(b);

Для каждого ребра (a, b) увеличиваем InDegree[b] на 1.

InDegree[b]++;

}

Все вершины с нулевой входящей степенью добавляем в очередь q.

for(i = 1; i < InDegree.size(); i++)

if (!InDegree[i]) q.push_back(i);

Продолжаем работу алгоритма, пока очередь q не пуста.

while(!q.empty())

{

Извлекаем вершину v из очереди и добавляем её в конец списка топологического порядка.

v = q.front(); q.pop_front();

top.push_back(v);

Удаляем из графа ребра (v, to). Для каждого такого ребра уменьшаем входящую степень вершины to.

for (int to : g[v])

{

InDegree[to]--;

Если входящая степень вершины to становится равной нулю, добавляем её в очередь. Впоследствии она будет помещена в список топологического порядка.

if (!InDegree[to]) q.push_back(to);

}

}

Если в массив top добавлены не все n вершин, то граф содержит цикл, и выполнить топологическую сортировку невозможно.

if (top.size() < n)

printf("-1\n");

else

{

В противном случае выводим вершины графа в порядке топологической сортировки.

for (int x : top) printf("%d ", x);

printf("\n");

}

Java реализация – поиск в глубину

import java.util.*;

import java.io.*;

public class Main

{

static ArrayList<ArrayList<Integer>> g;

static ArrayList<Integer> top = new ArrayList<Integer>();

static int used[];

static int n, m, flag = 0;

static void dfs(int v)

{

used[v] = 1;

for(int i = 0; i < g.get(v).size(); i++)

{

int to = g.get(v).get(i);

if (used[to] == 1) flag = 1;

if (used[to] == 0) dfs(to);

}

used[v] = 2;

top.add(v);

}

public static void main(String[] args)

{

FastScanner con = new FastScanner(System.in);

n = con.nextInt();

m = con.nextInt();

g = new ArrayList<ArrayList<Integer>>();

used = new int[n+1];

for (int i = 0; i <= n; i++)

g.add(new ArrayList<Integer>());

for (int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g.get(a).add(b);

}

for(int i = 1; i <= n; i++)

if (used[i] == 0) dfs(i);

if (flag == 1) System.out.println("-1");

else

for(int i = top.size() - 1; i >= 0; i--)

System.out.print(top.get(i) + " ");

System.out.println();

}

}

class FastScanner

{

BufferedReader br;

StringTokenizer st;

public FastScanner(InputStream inputStream)

{

br = new BufferedReader(new InputStreamReader(inputStream));

st = new StringTokenizer("");

}

public String next()

{

while (!st.hasMoreTokens())

{

try

{

st = new StringTokenizer(br.readLine());

} catch (Exception e)

{

return null;

}

}

return st.nextToken();

}

public int nextInt()

{

return Integer.parseInt(next());

}

}

Java реализация – Кан

import java.util.*;

import java.io.*;

public class Main

{

static ArrayList<ArrayList<Integer>> g;

static ArrayList<Integer> top;

static int InDegree[];

static int n, m, flag = 0;

public static void main(String[] args)

{

FastScanner con = new FastScanner(System.in);

n = con.nextInt();

m = con.nextInt();

g = new ArrayList<ArrayList<Integer>>();

InDegree = new int[n+1];

for (int i = 0; i <= n; i++)

g.add(new ArrayList<Integer>());

for (int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g.get(a).add(b);

InDegree[b]++;

}

Queue<Integer> q = new LinkedList<Integer>();

for(int i = 1; i <= n; i++)

if (InDegree[i] == 0) q.add(i);

top = new ArrayList<Integer>();

while (!q.isEmpty())

{

int v = q.poll();

top.add(v);

for (int to : g.get(v))

{

InDegree[to]--;

if (InDegree[to] == 0) q.add(to);

}

}

if (top.size() < n)

System.out.println("-1");

else

{

for (int x : top) System.out.print(x + " ");

System.out.println();

}

}

}

class FastScanner

{

BufferedReader br;

StringTokenizer st;

public FastScanner(InputStream inputStream)

{

br = new BufferedReader(new InputStreamReader(inputStream));

st = new StringTokenizer("");

}

public String next()

{

while (!st.hasMoreTokens())

{

try

{

st = new StringTokenizer(br.readLine());

} catch (Exception e)

{

return null;

}

}

return st.nextToken();

}

public int nextInt()

{

return Integer.parseInt(next());

}

}

Python реализация – поиск в глубину

Увеличим глубину рекурсии.

import sys

sys.setrecursionlimit(10000)

Функция dfs выполняет обход графа в глубину, начиная с вершины v.

def dfs(v):

Заходим в вершину v и помечаем её серым цветом.

used[v] = 1

Перебираем все вершины to, в которые можно попасть из вершины v.

for to in g[v]:

Если ориентированное ребро (v, to) ведет в серую вершину, это означает наличие цикла в графе. В этом случае устанавливаем flag = 1.

if used[to] == 1:

global flag

flag = 1

Если вершина to еще не посещена, рекурсивно запускаем из неё поиск в глубину.

if used[to] == 0:

dfs(to)

Завершаем обработку вершины v. Помечаем её чёрным цветом и добавляем в массив top.

used[v] = 2

top.append(v)

Основная часть программы. Читаем количество вершин n и количество ребер m.

n, m = map(int, input().split())

Входной граф храним в списке смежности g. Обьявим список used.

g = [[] for _ in range(n + 1)]

used = [0] * (n + 1)

Читаем список ребер. Строим список смежности графа.

for _ in range(m):

a, b = map(int, input().split())

g[a].append(b)

Выполняем обход ориентированного графа в глубину.

flag = 0

top = []

for i in range(1, n + 1):

if used[i] == 0: dfs(i)

Если при обходе в глубину обнаруживается цикл (установлен flag = 1), выводим -1.

if flag == 1:

print("-1")

else:

В противном случае выводим вершины графа в порядке, обратном их добавлению в массив top.

for i in range(len(top) - 1, -1, -1):

print(top[i], end=" ")

print()

Python реализация – алгоритм Кана

Объявим очередь q.

from collections import deque

q = deque()

Читаем количество вершин n и количество ребер m.

n, m = map(int, input().split())

Входной граф храним в списке смежности g.

Входящие степени вершин храним в списке InDegree.

Результат топологической сортировки заносим в список top.

g = [[] for _ in range(n + 1)]

InDegree = [0] * (n + 1)

top = []

Читаем m ребер графа.

for _ in range(m):

a, b = map(int, input().split())

g[a].append(b)

Для каждого ребра (a, b) увеличиваем InDegree[b] на 1.

InDegree[b] += 1

Все вершины с нулевой входящей степенью добавляем в очередь q.

for i in range(1, len(InDegree)):

if not InDegree[i]: q.append(i)

Продолжаем работу алгоритма, пока очередь q не пуста.

while q:

Извлекаем вершину v из очереди и добавляем её в конец списка топологического порядка.

v = q.popleft()

top.append(v)

Удаляем из графа ребра (v, to). Для каждого такого ребра уменьшаем входящую степень вершины to.

for to in g[v]:

InDegree[to] -= 1

Если входящая степень вершины to становится равной нулю, добавляем её в очередь. Впоследствии она будет помещена в список топологического порядка.

if not InDegree[to]: q.append(to)

Если в массив top добавлены не все n вершин, то граф содержит цикл, и выполнить топологическую сортировку невозможно.

if len(top) < n:

print("-1")

else:

В противном случае выводим вершины графа в порядке топологической сортировки.

for i in top:

print(i, end=" ")

print()